
| OPA Lattice Design Code |

|
The screen shots below show some of OPA's features. For more information please consult the user guide (PDF).
OPA reads and writes ascii text files for the lattices, which can be edited manually by any editor, or inside OPA using a simple Text Editor. Alternatively the OPA editor can be used to create, edit or delete elements and segments. Any segment then can be chosen to be the active segment to become the lattice to work with.

Usually one starts here after loading a lattice file: The linear optics panel displays beta functions and dispersion and the most important lattice parameters:
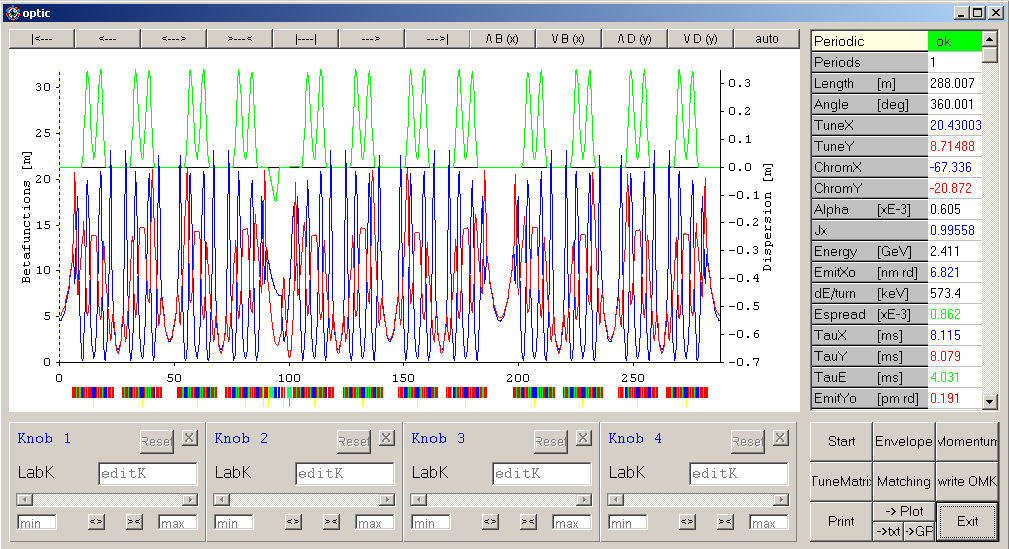
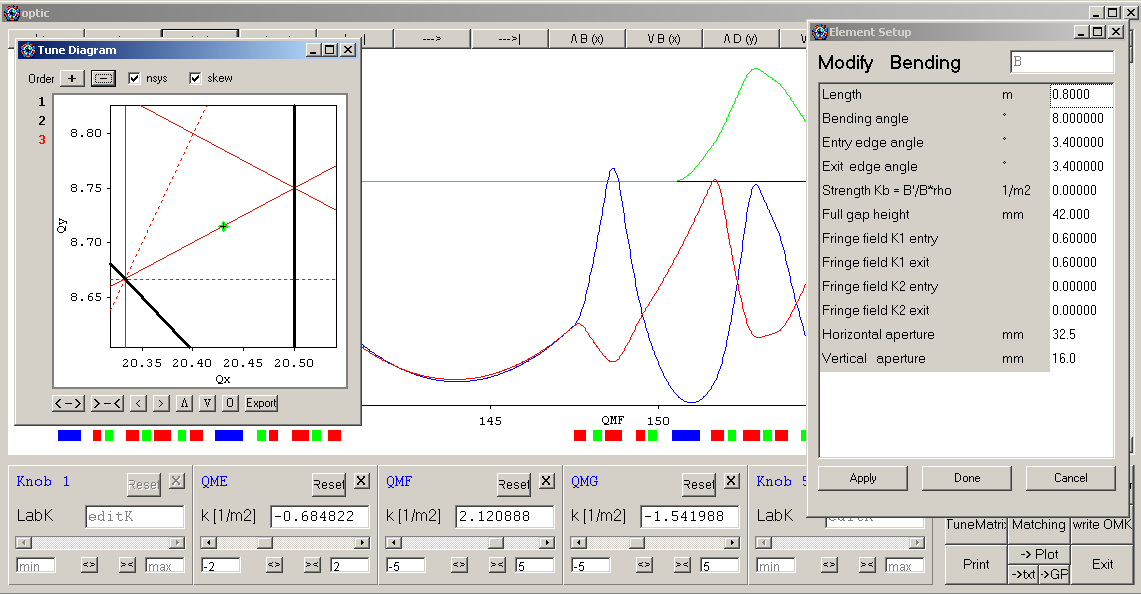
A tune diagram pops up if there is a periodic solution. Elements can be dragged to knobs or double-clicked to open the element setup panel:
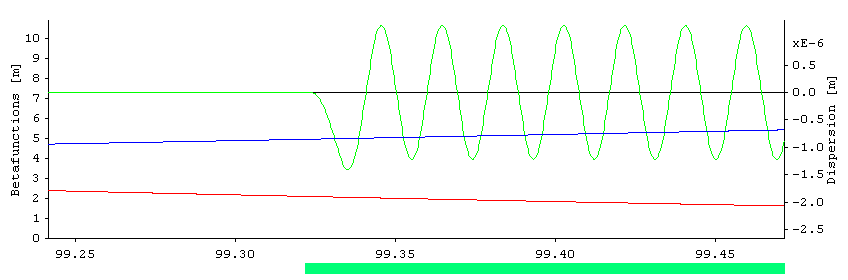
Buttons at top allow to scale and zoom in: Internally, elements are divided in slices of a maximum length corresponding to one pixel at the screen, so the optical functions inside an element can be resolved. For example, view the dispersion inside an undulator:
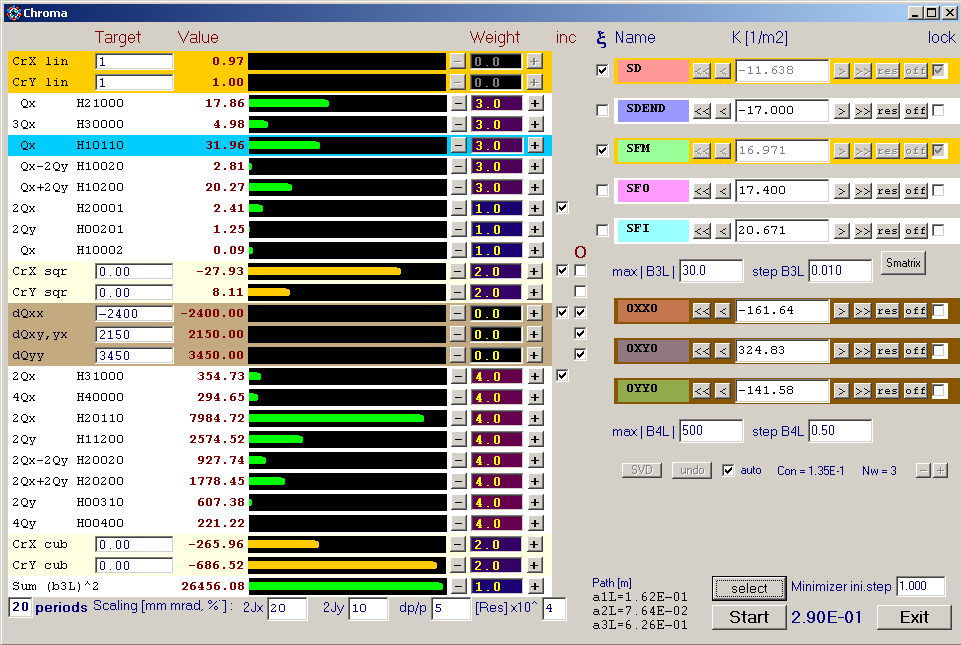
The Hamiltonian modes for 1st and 2nd order in sextupole strength and for 1st order in octupole strengths are calculated and displayed by absolute values. Chromaticities up to 3rd order are obtained by numerical differentiation of the closed orbit. For phase independent terms like chromaticities and amplitude dependent tune shifts (ADTS), target values can be given. The green bars are the Hamiltonian modes scaled by realistic values of betatron amplitudes and momentum deviation entered at the bottom line, and by the weight factors. They represent contributions to a penalty function which can be minimized numerically. Linear chromaticities can be locked by selecting two sextupole families to keep their values constant during minimization. 2nd order chromaticities and ADTS can be fixed in the same way by activating a linear solver (SVD) for the octupole families.
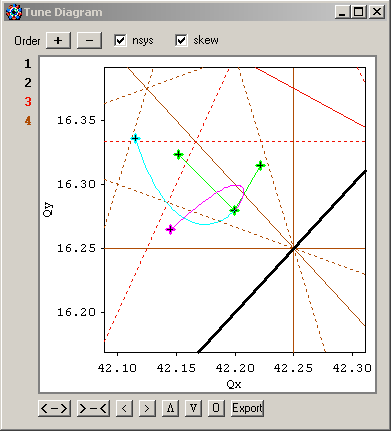
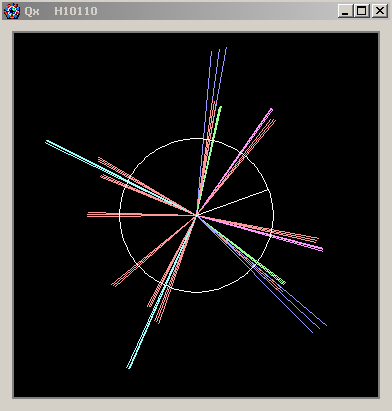
A tune diagram will show a prediction for the beam footprint based on the values of chromaticities and ADTS. The select button opens a window showing the star diagram of complex vectors for the first order sextupole modes (the multiple lines indicate the single kicks from modeling a thick sextupoles):
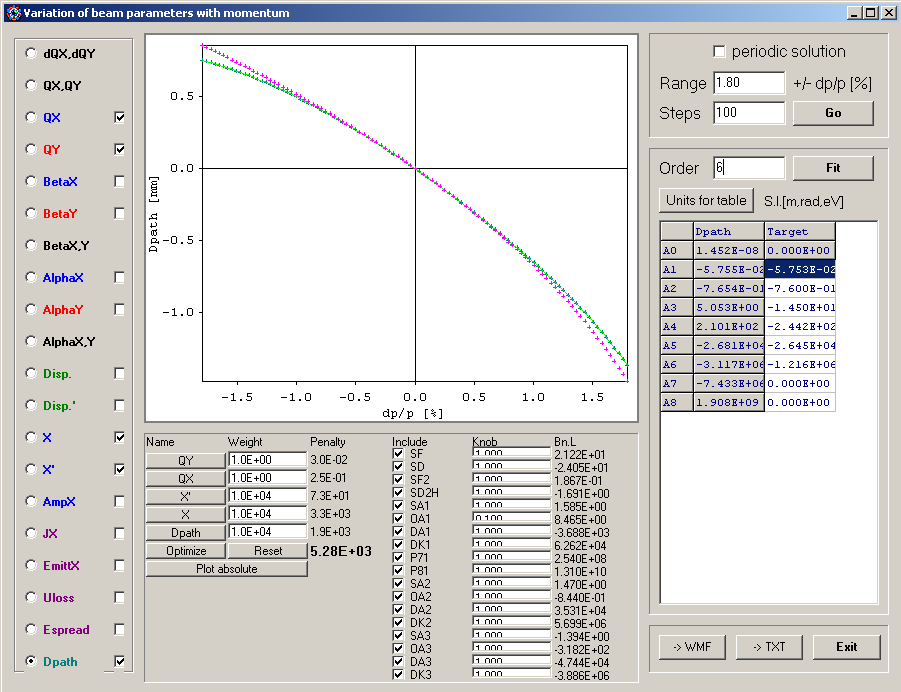
Various lattice parameters as a function of momentum can be displayed with the panel below. A minimizer allows to adjust a set of parameters to target function entered by polynomial coefficients:
Starting coordinates of a particle can be entered in the corresponding fields or simply by clicking into the figures. The track point can be anywhere, even inside an element. Fourier spectra are calculated from the particle's motion and peaks are identified:
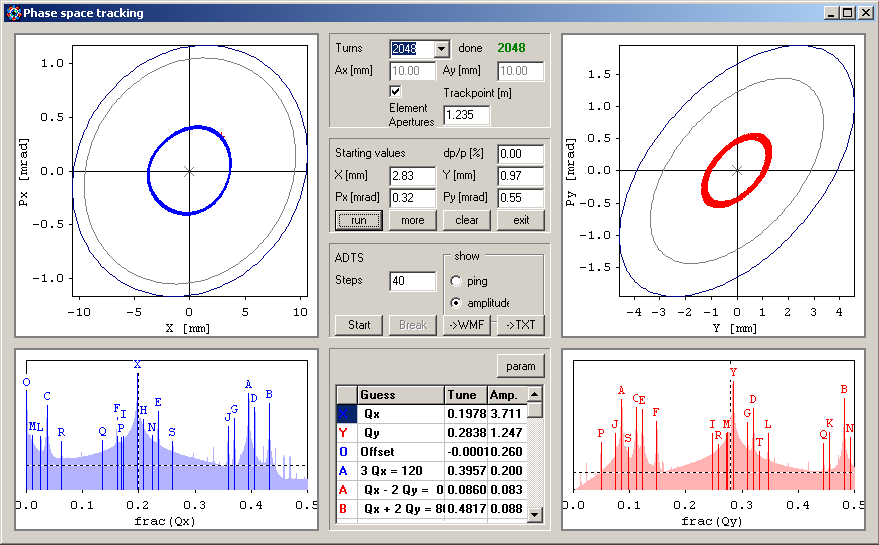
To determine amplitude dependent tune shifts (ADTS), the particle amplitudes are stepped up (simulating a pinger) while the fundamental tune is tracked in the FFT. This is done for horizontal, coupled and vertical amplitudes. The results are compared to the analytic results (solid lines in left figure below), if these were calculated before by the non-linear optimization module. The results are also shown in the tune diagram
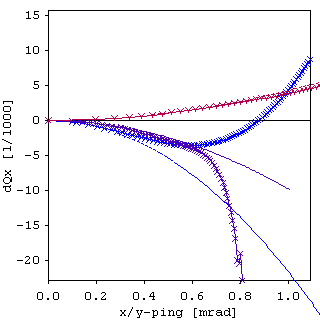
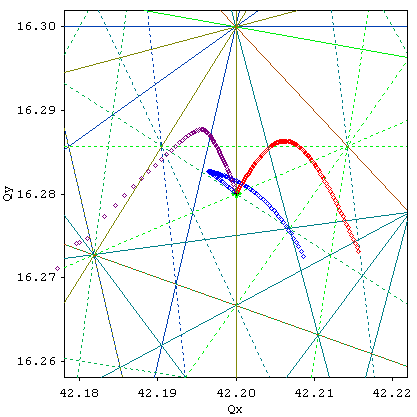
- - by the way, double-clicking in any plot (except the linear optics plot above) copies it to the Windows clip board. - -
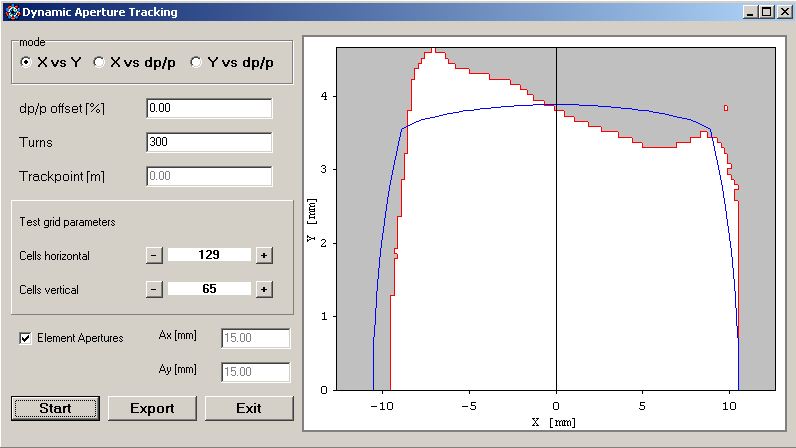
For tracking dynamic aperture OPA uses a grid to probe the aperture which is refined in steps, so one can early see if the result is bad and stop the calculation. The blue line in the figure below shows the projection of the beampipe to the trackpoint from linear optics using local element apertures and assuming elliptical cross sections. The red line is the dynamic aperture obtained from tracking:
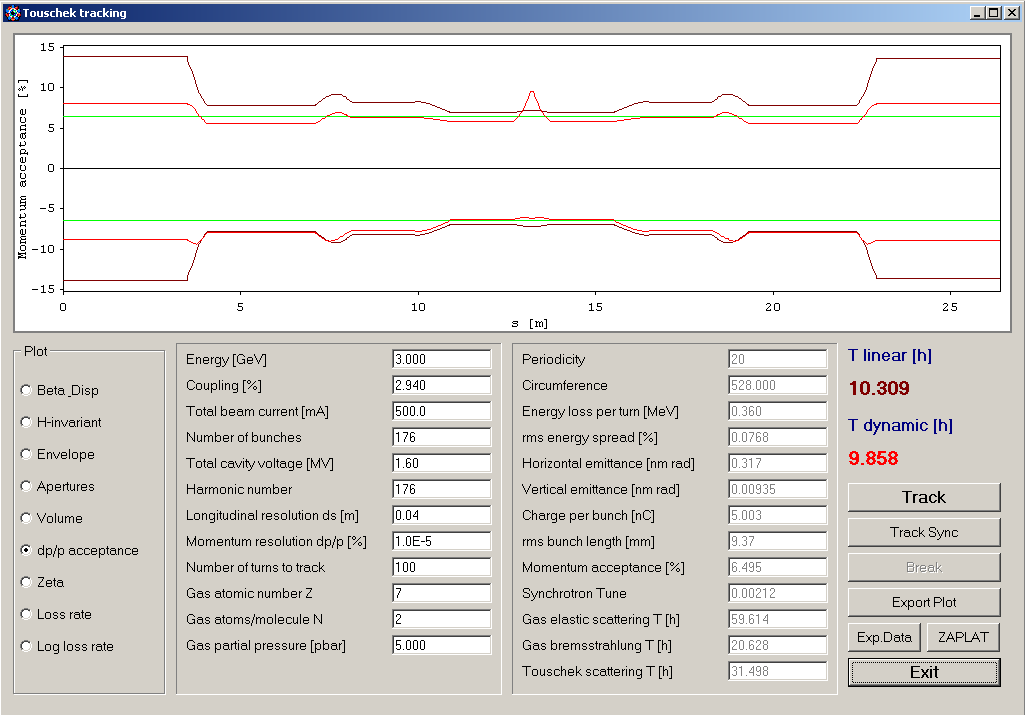
Local losses due to Touschek scattering depend on the local momentum acceptance, which is the minor of the RF momentum acceptance (green line in figure below), the local projection of the horizontal geometric acceptance (brown) and the local projection of the horizontal dynamic acceptance (red). The latter is obtained from tracking:
- - want see more? - - download and play!