


Next: MEDIUM AND LONG TERM
Up: SHORT TERM STABILITY
Previous: SHORT TERM STABILITY
Orbit feedbacks can be divided in two classes:
- Global feedbacks compensate for perturbations generated by all IDs based on global orbit and/or photon beam positions by means of global correction.
- Local feedbacks compensate for perturbations generated by individual IDs based on local orbit and/or photon beam positions by means of local correction in the vicinity of the IDs.
In both cases a certain global reference orbit often referred to as the ``golden orbit'' needs to be established. Preferably this orbit is going through the centers of quadrupoles and sextupoles in order to minimize optics distortions which lead to spurious vertical dispersion and betatron coupling and thus an increased emittance coupling. Usually some extra steering in the vicinity of the IDs is added. In order to find this orbit ``beam-based calibration'' techniques [9] need to be employed which determine the offset of the BPM zero reading with respect to the magnetic center of the adjacent quadrupole. This offset is determined by altering the focusing 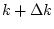 of individual quadrupoles and measuring the resulting RMS orbit change which is determined by the product of the known
of individual quadrupoles and measuring the resulting RMS orbit change which is determined by the product of the known 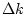 and the initial orbit excursion at the location of the modulated quadrupole. A comparison with the corresponding reading of the adjacent BPM reveals the offset. Even for well aligned machines these offsets can be of the order of a few 100
and the initial orbit excursion at the location of the modulated quadrupole. A comparison with the corresponding reading of the adjacent BPM reveals the offset. Even for well aligned machines these offsets can be of the order of a few 100 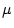 m [10] since they represent a convolution of mechanical and electronical properties of the BPMs. As a result the remaining DC RMS corrector strength is usually significantly reduced when correcting to the ``golden orbit''.
The correlation between correctors and BPMs is established by superimposing the BPM pattern for the excitation of every single corrector. Very often the horizontal and vertical plane are treated independently assuming a small betatron coupling. The coefficients of the two resulting correlation matrices also called response matrices can be derived analytically from the machine model or from orbit measurements. To turn this into a correction algorithm it is necessary to ``invert'' the matrices in order to get the corrector pattern as a function of a given BPM pattern. If the correlation matrix is a square
m [10] since they represent a convolution of mechanical and electronical properties of the BPMs. As a result the remaining DC RMS corrector strength is usually significantly reduced when correcting to the ``golden orbit''.
The correlation between correctors and BPMs is established by superimposing the BPM pattern for the excitation of every single corrector. Very often the horizontal and vertical plane are treated independently assuming a small betatron coupling. The coefficients of the two resulting correlation matrices also called response matrices can be derived analytically from the machine model or from orbit measurements. To turn this into a correction algorithm it is necessary to ``invert'' the matrices in order to get the corrector pattern as a function of a given BPM pattern. If the correlation matrix is a square 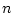 x
x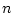 matrix and has
matrix and has 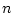 independent eigenvectors and is not ill-conditioned this is easy to accomplish and one gets a unique solution for the problem by matrix inversion. In reality the number of correctors and BPMs can be already different by design or due to BPM failures and magnet saturations. As a result the matrix is non-square and the solution is no longer unique. A very flexible way to handle these scenarios is offered by the SVD algorithm [11]. This numerically very robust method minimizes the RMS orbit and the proposed RMS corrector strength changes at the same time if the number of correctors is larger than the number of BPMs whilst the RMS orbit is minimized in the reverse case. By introducing cutoffs in the eigenvalue spectrum for small eigenvalues only the most effective corrector combinations are selected and the correction gets less sensitive to BPM errors [12]. Thus this technique makes ``Most Effective Corrector'' and ``MICADO'' like long range correction schemes superfluous. Since modern light sources are built with very tight alignment tolerances and BPMs are well calibrated with respect to adjacent quadrupoles, orbit correction by matrix inversion in the
independent eigenvectors and is not ill-conditioned this is easy to accomplish and one gets a unique solution for the problem by matrix inversion. In reality the number of correctors and BPMs can be already different by design or due to BPM failures and magnet saturations. As a result the matrix is non-square and the solution is no longer unique. A very flexible way to handle these scenarios is offered by the SVD algorithm [11]. This numerically very robust method minimizes the RMS orbit and the proposed RMS corrector strength changes at the same time if the number of correctors is larger than the number of BPMs whilst the RMS orbit is minimized in the reverse case. By introducing cutoffs in the eigenvalue spectrum for small eigenvalues only the most effective corrector combinations are selected and the correction gets less sensitive to BPM errors [12]. Thus this technique makes ``Most Effective Corrector'' and ``MICADO'' like long range correction schemes superfluous. Since modern light sources are built with very tight alignment tolerances and BPMs are well calibrated with respect to adjacent quadrupoles, orbit correction by matrix inversion in the 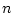 x
x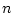 case which is equivalent to an SVD employing all eigenvalues has become an option since the resulting RMS corrector strength is still moderate (typically
case which is equivalent to an SVD employing all eigenvalues has become an option since the resulting RMS corrector strength is still moderate (typically 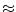 100
100 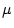 rad), BPMs are reliable and their noise is small (no BPM averaging is performed which is similar to a local feedback scenario). This allows to establish any desired ``golden orbit'' within the limitations of the available corrector strength and the residual corrector/BPM noise.
For the horizontal orbit correction it is crucial to take into account path-length effects due to circumference or rf frequency changes by correcting the corresponding dispersion orbits by means of the rf frequency. A gradual build-up of a dispersion related corrector pattern with a nonzero mean must be avoided since this leads together with an rf frequency change to a corrected orbit at a different beam energy. Thus it is desirable to subtract the pattern from the actual corrector settings before orbit correction in order to remove this ambiguity.
In order to implement a global orbit feedback based on the described algorithm which stabilizes the electron beam with respect to the established ``golden orbit'' up to frequencies
rad), BPMs are reliable and their noise is small (no BPM averaging is performed which is similar to a local feedback scenario). This allows to establish any desired ``golden orbit'' within the limitations of the available corrector strength and the residual corrector/BPM noise.
For the horizontal orbit correction it is crucial to take into account path-length effects due to circumference or rf frequency changes by correcting the corresponding dispersion orbits by means of the rf frequency. A gradual build-up of a dispersion related corrector pattern with a nonzero mean must be avoided since this leads together with an rf frequency change to a corrected orbit at a different beam energy. Thus it is desirable to subtract the pattern from the actual corrector settings before orbit correction in order to remove this ambiguity.
In order to implement a global orbit feedback based on the described algorithm which stabilizes the electron beam with respect to the established ``golden orbit'' up to frequencies 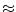 100 Hz BPM data acquisition rates of at least
100 Hz BPM data acquisition rates of at least 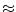 1-2 kHz are needed. If sub-micron in-loop orbit stability is required the integrated noise contribution from the BPM electronics must not exceed a few hundred nanometers which is achieved with modern digital four channel (parallel) BPM [13] as well as analog multiplexed systems [14]. A fast network needs to be established which distributes the acquired BPM data around the ring or to a central point in order to be able to determine the individual correction values which in general depend on all BPM readings. Since the necessary matrix multiplications with the BPM vector can be parallelized a distribution on several CPU units handling groups of correctors is a natural solution. Furthermore the ``inverted'' matrix can be sparse depending on the BPM/corrector layout such that most of the off-diagonal coefficients are zero. In these cases only a small subset of all BPM readings in the vicinity of the individual correctors determines their correction values. At the SLS where all 72 BPMs have adjacent correctors in both planes and the phase advance between correctors is
1-2 kHz are needed. If sub-micron in-loop orbit stability is required the integrated noise contribution from the BPM electronics must not exceed a few hundred nanometers which is achieved with modern digital four channel (parallel) BPM [13] as well as analog multiplexed systems [14]. A fast network needs to be established which distributes the acquired BPM data around the ring or to a central point in order to be able to determine the individual correction values which in general depend on all BPM readings. Since the necessary matrix multiplications with the BPM vector can be parallelized a distribution on several CPU units handling groups of correctors is a natural solution. Furthermore the ``inverted'' matrix can be sparse depending on the BPM/corrector layout such that most of the off-diagonal coefficients are zero. In these cases only a small subset of all BPM readings in the vicinity of the individual correctors determines their correction values. At the SLS where all 72 BPMs have adjacent correctors in both planes and the phase advance between correctors is 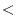 180
180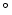 the structure of the inverted 72x72 matrix resembles a correction with interleaved closed orbit bumps made up from three successive correctors [15]. The feedback loop is usually closed by means of a PID controller function optimizing gain, bandwidth and stability of the loop (see Figure 5). Notch filters allow to add additional ``harmonic suppression'' [16,17] of particularly strong lines in the noise spectrum.
the structure of the inverted 72x72 matrix resembles a correction with interleaved closed orbit bumps made up from three successive correctors [15]. The feedback loop is usually closed by means of a PID controller function optimizing gain, bandwidth and stability of the loop (see Figure 5). Notch filters allow to add additional ``harmonic suppression'' [16,17] of particularly strong lines in the noise spectrum.
Figure 5:
Fast orbit feedback closed loop transfer functions in the horizontal (blue) and vertical (red) plane at the SLS. Damping is achieved up to 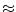 100 Hz [5].
100 Hz [5].
|
|
The effect of the minimum applicable correction strength which is defined by the PS resolution for a given current range must be within the BPM noise and is typically of the order 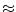 10 nrad corresponding to
10 nrad corresponding to 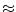 18 bit (
18 bit (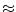 4 ppm) resolution for a PS with
4 ppm) resolution for a PS with 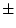 1 mrad maximum strength. Modern PS with digital control have reached noise figures of
1 mrad maximum strength. Modern PS with digital control have reached noise figures of 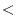 1 ppm providing kHz small-signal bandwidth [18] which opens the possibility to use the same correctors for DC and fast correction. Eddy currents induced in the vacuum chamber should not significantly attenuate or change the phase of the effective corrector field up to the data acquisition rate. Since eddy currents are proportional to the thickness and electrical conductivity of materials, only thin laminations (
1 ppm providing kHz small-signal bandwidth [18] which opens the possibility to use the same correctors for DC and fast correction. Eddy currents induced in the vacuum chamber should not significantly attenuate or change the phase of the effective corrector field up to the data acquisition rate. Since eddy currents are proportional to the thickness and electrical conductivity of materials, only thin laminations (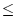 1 mm thickness) or air coils should be used for correctors and low conductive materials preferred for vacuum chambers. Eddy currents in vacuum chambers usually impose the most critical bandwidth limitation on the feedback loop. Global fast orbit feedbacks are operational or have been proposed for a large number of light sources, see Table 2. ALS [14], APS [20], ESRF [21], NSLS [17], SLS [5] and Super-ACO [22] (operated
1 mm thickness) or air coils should be used for correctors and low conductive materials preferred for vacuum chambers. Eddy currents in vacuum chambers usually impose the most critical bandwidth limitation on the feedback loop. Global fast orbit feedbacks are operational or have been proposed for a large number of light sources, see Table 2. ALS [14], APS [20], ESRF [21], NSLS [17], SLS [5] and Super-ACO [22] (operated  12/03) have running configurations in user operation. BESSY [23], DELTA [24], SPEAR3 [25] and SPring-8 [26] have proposals, some of them [24,26] test setups. The upcoming machines DIAMOND [27] and SOLEIL [6] have proposals for fast global orbit feedbacks.
12/03) have running configurations in user operation. BESSY [23], DELTA [24], SPEAR3 [25] and SPring-8 [26] have proposals, some of them [24,26] test setups. The upcoming machines DIAMOND [27] and SOLEIL [6] have proposals for fast global orbit feedbacks.
Table:
Compilation of operational global, proposed global and operational local fast orbit feedback systems at light sources (adapted from [19])
| SR Facility |
BPM Type |
max. BW |
Stability |
|---|
| ALS |
RF-BPMs |
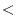 50 Hz 50 Hz |
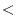 1 1 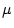 m m |
|---|
| APS |
RF&X-BPMs |
50 Hz |
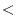 1 1 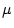 m m |
|---|
| ESRF |
RF-BPMs |
100 Hz |
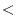 0.6 0.6 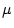 m m |
|---|
| NSLS |
RF&X-BPMs |
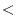 200 Hz 200 Hz |
1.5 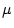 m m |
|---|
| SLS |
RF&X-BPMs |
100 Hz |
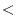 0.3 0.3 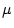 m m |
|---|
| Super-ACO |
RF-BPMs |
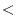 150 Hz 150 Hz |
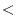 5 5 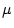 m m |
|---|
| BESSY |
RF-BPMs |
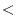 100 Hz 100 Hz |
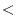 1 1  m m |
| DELTA |
RF-BPMs |
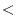 150 Hz 150 Hz |
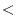 2 2 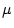 m m |
| DIAMOND |
RF-BPMs |
150 Hz |
0.2 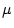 m m |
| SOLEIL |
RF-BPMs |
150 Hz |
0.2 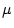 m m |
| SPEAR3 |
RF-BPMs |
100 Hz |
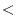 3 3 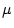 m m |
| SPring-8 |
RF-BPMs |
100 Hz |
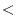 1 1 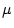 m m |
| APS |
X-BPMs |
50 Hz |
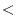 1 1 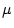 m m |
| BESSY |
X-BPMs |
50 Hz |
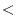 1 1 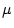 m m |
| ELETTRA |
RF-BPMs |
80 Hz |
0.2 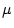 m m |
Local fast orbit feedbacks (see Table 2) stabilize orbit position and angle at ID centers locally without effecting the orbit elsewhere which is accomplished by a superposition of symmetric and asymmetric closed orbit bumps consisting of 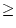 4 correctors per plane around the ID. Photon BPMs (X-BPMs) which are located in the beam line frontends measuring photon beam positions provide very precise information about orbit fluctuations at the ID source point at a typical bandwidth of
4 correctors per plane around the ID. Photon BPMs (X-BPMs) which are located in the beam line frontends measuring photon beam positions provide very precise information about orbit fluctuations at the ID source point at a typical bandwidth of 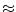 2 kHz. With two X-BPMs position and angle fluctuations can be disentangled. Unfortunately the reading depends on the photon beam profile and thus on the individual ID settings. APS is operating X-BPM based feedbacks on their dipole and ID X-BPMs at fixed gap [20]. BESSY has the prototype for an X-BPM based feedback on an APPLE II ID [23]. ELETTRA implemented a feedback for an electromagnetic elliptical wiggler (EEW) based on a new type of digital ``low gap'' BPM [16]. If several global and/or local feedbacks are operated they need to be decoupled. Either they are well separated in frequency which evidently leads to correction dead bands [20] or they run in a cascaded master-slave configuration [28,20,14,5].
2 kHz. With two X-BPMs position and angle fluctuations can be disentangled. Unfortunately the reading depends on the photon beam profile and thus on the individual ID settings. APS is operating X-BPM based feedbacks on their dipole and ID X-BPMs at fixed gap [20]. BESSY has the prototype for an X-BPM based feedback on an APPLE II ID [23]. ELETTRA implemented a feedback for an electromagnetic elliptical wiggler (EEW) based on a new type of digital ``low gap'' BPM [16]. If several global and/or local feedbacks are operated they need to be decoupled. Either they are well separated in frequency which evidently leads to correction dead bands [20] or they run in a cascaded master-slave configuration [28,20,14,5].



Next: MEDIUM AND LONG TERM
Up: SHORT TERM STABILITY
Previous: SHORT TERM STABILITY
Michael Boege
2004-07-12
![\includegraphics* [width=1.\linewidth=3.0]{THXCH01f5.eps}](img34.gif)
![\includegraphics* [width=1.\linewidth=3.0]{THXCH01f5.eps}](img34.gif)