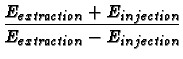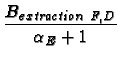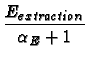Next: Application to the SLS
Up: Eddy current effects in
Previous: The SLS Booster
Theoretical background
The ramping cycle of the booster is determined by the time-dependent
dipolar field of the bending magnets. These fields follows a
biased-sine shape given by:
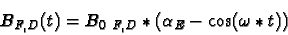 |
(1) |
where 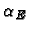 and
and
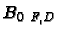 determine the minimum and maximum
energy possible in the booster. In the SLS case, the beam is injected
at the minimum energy of the ramping cycle, and extracted at the
maximum. The energy ramp is:
determine the minimum and maximum
energy possible in the booster. In the SLS case, the beam is injected
at the minimum energy of the ramping cycle, and extracted at the
maximum. The energy ramp is:
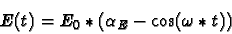 |
(2) |
And the parameters
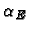 ,
,
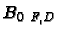 and E0 are given
by::
and E0 are given
by::
The time dependent fields produce eddy currents in the vacuum chamber
of the bending magnet. These currents create a distortion of the
magnetic field inside the vacuum chamber. In the center of the pipe,
the distortion of the dipolar magnetic field is a decrease of the
field, given by:
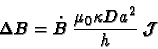 |
(6) |
where 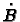 is the temporal derivative of the corresponding
BF,D(t) field,
is the temporal derivative of the corresponding
BF,D(t) field, 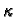 the conductivity of the vacuum chamber,
D its thickness and 2h the magnet gap. The parameters a and bare the horizontal and vertical half apertures of the vacuum chamber.
the conductivity of the vacuum chamber,
D its thickness and 2h the magnet gap. The parameters a and bare the horizontal and vertical half apertures of the vacuum chamber.
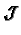 is a form factor given by:
is a form factor given by:
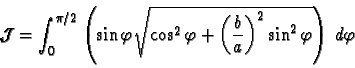 |
(7) |
For a round vacuum pipe (a=b),
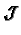 is 1. in the SLS case,
b/a=2/3, and
is 1. in the SLS case,
b/a=2/3, and
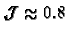 .
.
The analysis of this field distortion shows[1] that it can
be expressed as a sextupolar time-dependent component given by:
If we replace in equation 8 the values of the
time-dependent magnetic field( equation 1) and its
derivative, we obtain the following expression for the the sextupolar
component:
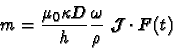 |
(9) |
If we rearrange the terms in this last equation, we can write it as:
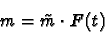 |
(10) |
where 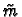 is a constant, given by:
is a constant, given by:
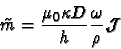 |
(11) |
and F(t) contains the dependence in time:
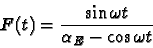 |
(12) |
The function F(t) is plotted in figure 2. As show in the
plot, the sextupolar contribution will be more important at the start
of the ramping cycle (low energies).
Figure 2:
Plot of F(t) for the SLS booster parameters (3 Hz repetition rate,
Emin= 0.1 GeV and Emax= 2.4 GeV.)
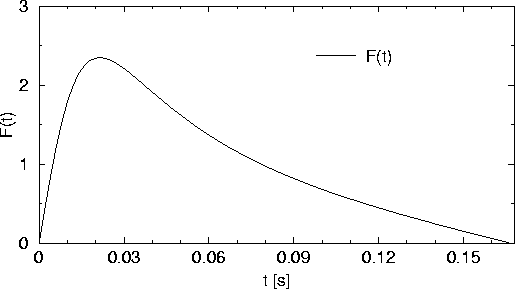 |



Next: Application to the SLS
Up: Eddy current effects in
Previous: The SLS Booster
Marc Munoz
1998-11-18